
A shear wall design is complete when assemblage configuration design step, moment design step, and shear design step have been performed. Upon the completion of a design (whether it be successful or not), users have access to several output tabs. MASS is exceptionally transparent, providing the opportunity to quickly see exactly what equations the program used to achieve the design. This is extremely beneficial not only to users but to other designers that may review users’ work. As part of the results, the program provides detailed drawings that reflect the completed design, including: shear wall, loads, reactions, moment, shear, and P-M diagram drawings. The program also provides tabulated results. There are three result categories available for each module: simplified results, detailed results, and loads analysis results. The three result categories vary in the amount of detail provided, but all contain separate tables that approximately correspond to each design step. All drawings and results can be readily printed.
All results explored in this section assume a completed shear wall design. The drawings and tabulated results are often available in advance of a completed solution. The availability of a specific drawing or tabulated result is mentioned at each step during the design procedure (discussed in Section 5.2).
There are several useful drawings that the program provides in the shear wall module including, Shear Wall, Loads, Reactions, Moment, Shear, and the P-M Diagram.
The first drawing become available as soon as the assemblage configuration design step is complete. The loads, reactions, moment, and shear drawing are not available until the loads input design step is performed. The P-M diagram is not available until the moment design step is performed. The out-of-plane drawing is updated at each design step to reflect any changes made to the assemblage. The drawings are not complete until all the design steps have been performed.
The assemblage drawing displays a drawing of the assemblage based on the material properties selected by users. The drawing displays the dimensions of the assemblage, as well as the detailed layout of the masonry units used in the design. To view the shear wall drawing:
For the shear wall module, all drawings are displayed in the right window, with the dimensions (height, length, width) of the shear wall clearly labelled, as shown in Figure 5‑78: Shear Wall Drawing . The shear wall drawing includes the front view of the assemblages, as well as a top or cross-sectional view of the shear wall.

Figure 5‑78: Shear Wall Drawing
In the front view, the drawing provides the length and height of the shear wall, as well as the width of each flange (if applicable). The vertical, black line of mortar next to the end units denotes the presence of a flange. The placement of the vertical and horizontal reinforcement steel (if applicable) is also shown. Horizontal bars are drawn approximately one-third of way from the top of the bond beam course, simulating the placement of horizontal reinforcement at a knockout depth of 100 mm. Joint reinforcement is drawn at the bed joints. Reinforcing bars normally extend out of the wall into the story above or other adjacent elements, in the program the bars are modelled as extending exactly to the end of the wall, no bends or hooks area shown.
Warning: In the shear wall drawing, the vertical steel extends up to the ends of the wall as not to deceive users into thinking that the development length calculations had been performed. MASS does not perform any detailing work.
Shear walls that require cut units are outlined in red in both views. For shear walls that are not modular in height or in web length cut-off blocks are to be highlighted in red to indicate a constructability concern. Cut-off blocks should be placed and highlighted at the top of the shear wall (in case of a non-modular height) and at the right side of the web of the shear wall (in the case of a non-modular web length). The program always forces the left side of the wall to start at either the end of a unit or at the half length of a unit. The program always forces the bottom side of the wall to start at either the end of a unit or at the half length of a unit.
In the cross-sectional view, the widths, and lengths of the web and the flanges (if applicable) are shown. In addition, the grouting pattern and the placement of the vertical steel is shown in more detail. Assemblages that require cut units are outlined in red in the cross-sectional view as well. This allows users to readily see the cut units within the flanges (if applicable).
The shear wall drawing is updated at each design step to reflect any changes made to the design. Upon the completion of the moment design for instance, the assemblage displays the steel that has been placed along the length of the assemblage. In the case of shear walls, a cross-sectional drawing along the top of the shear wall is also drawn, and includes the placement of the vertical reinforcing steel.
Warning: In the shear wall drawing, the vertical steel extends up to the ends of the wall as not to deceive users into thinking that the development length calculations had been performed. MASS does not perform any detailing work.
The loads drawing displays the loads that are applied to the shear wall. It is completed during the loads input design step. To view the loads drawing:
A specific applied load can be viewed under the Loads tab by clicking on the box of that particular load (under the ‘Selected load’ column). Multiple loads can be viewed by holding down Shift key, and selecting the loads to be displayed. Figure 5‑79: Loads Drawing ‑ shows four selected applied loads that are displayed in the loads drawing. The applied loads that are selected are highlighted in blue.
Each load type applied is displayed using a different colour. The dead load is displayed in red, and the live load is displayed in green.
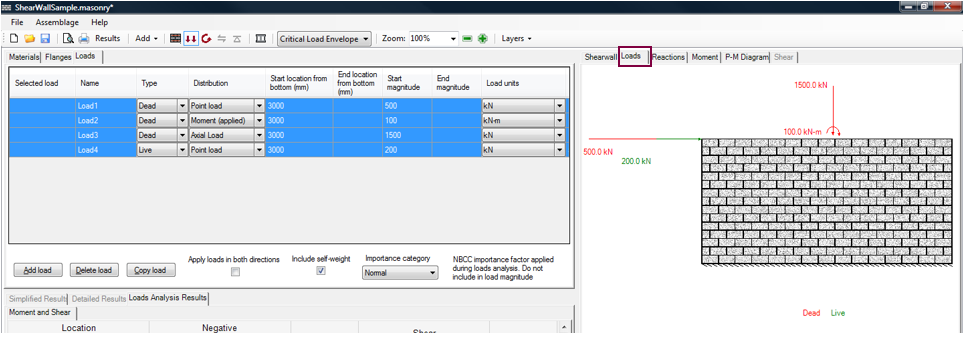
Figure 5‑79: Loads Drawing
A full list of all load types available in the shear wall module, as well as their corresponding colour, are listed in Table 5‑2: Load Type Colour Convention ‑.
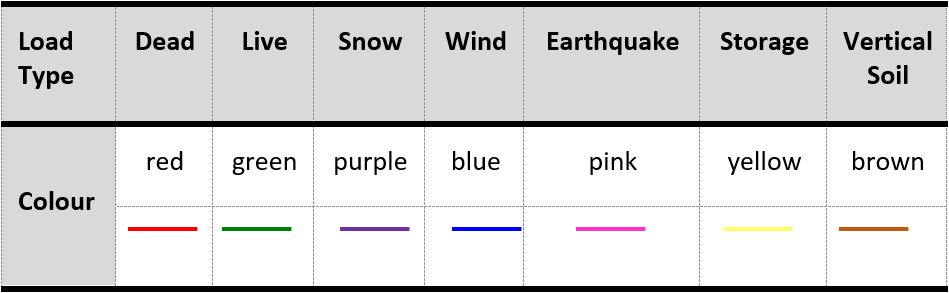
Table 5‑2: Load Type Colour Convention
The reactions drawing displays the support reactions that are applied to the shear wall due to a chosen load combination. It is completed during the loads input design step. The drawing is updated at each design step to reflect any changes made to the assemblage. A change in the masonry unit size for instance, affects the self-weight of the shear wall, and thus the resulting support reactions.
To view the reactions drawing:

Figure 5‑80: Reactions Drawing
By default, the reactions drawing displayed uses the critical load envelope (formed by the worst case of all load combinations at any point in the shear wall). Reactions due to specific load combinations can be viewed by clicking on the Critical Load Envelope drop-down box. The drawing indicates in the top left corner the load combination used to determine that specific reaction.
Reaction forces (as well as moment and shear curves) are displayed using red, green, or both. A red reaction force indicates a negative reaction force (east to west). A green reaction force indicates a positive reaction force (west to east).
Moment reaction arrows follow a similar scheme. A red moment arrow at the top end of the wall indicates a positive moment reaction (counter-clockwise). A green arrow at the top end of the wall indicates a negative moment reaction (clockwise). A red arrow at the base of the wall indicates a positive moment reaction (clockwise). A green arrow at the base of the wall indicates a negative moment reaction (counter-clockwise).
The moment drawing displays the moment applied along the height of the shear wall due to the applied loads and moments of a chosen load combination. It is completed during the loads input design step. The drawing is updated at each design step to reflect any changes made to the assemblage. A change in the masonry unit size for instance, affects the self-weight of the shear wall, the resulting support reactions, and thus the applied moment.
To view the moment drawing:
The bending moment diagram for a typical case of uniform positive bending, for a fixed-free supported shear wall is shown in Figure 5‑81: Moment diagram ‑.
By default, the moment drawing displayed uses the critical load combination.
A moment corresponding to a specific load combination can be viewed by clicking on the Critical Load Envelope drop-down box. The drawing indicates at the top left corner the load combination used to determine that specific moment diagram.
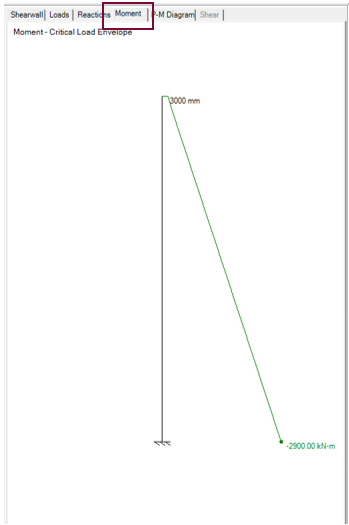
Figure 5‑81: Moment diagram
For the ‘Critical Load Envelope’ selection only, moment diagrams are displayed using red, green, or both. A red moment curve identifies a positive moment (in tension). A green moment curve identifies a negative moment (in compression). Maximum absolute positive and negative moments are indicated as dots, (unless the maximum absolute moment is zero, i.e. there is no negative moment.) For all other load combinations the moment diagrams are displayed using a red curve.
The shear drawing displays the shear applied along the height of the shear wall due to the applied loads and moments of a chosen load combination. It is first displayed during the loads input design step. The drawing is updated at each design step to reflect any changes made to the shear wall.
To view the shear drawing:
A shear diagram for a fixed-free supported shear wall is shown in Figure 5‑82: Shear diagram ‑.
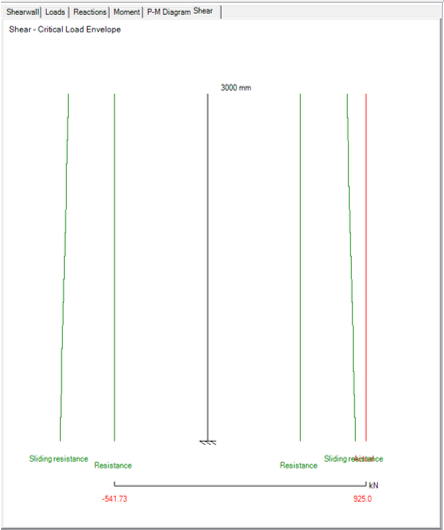
Figure 5‑82: Shear diagram
The shear diagram corresponding to a specific load combination can be viewed by clicking on the Critical Load Envelope drop-down box. The drawing indicates at the top left corner the load combination used to determine that specific shear diagram.
Completing the shear design step updates the shear drawing. In addition the actual (applied) shear displayed at the loads input design stage, the design shear and shear resistance curves are also displayed, as shown in Figure 5‑82: Shear diagram ‑.
The actual shear is the shear the shear wall experiences due to the applied loads and moments. This curve is determined by the loads analysis engine, and is plotted, in red, between the centres of support. The design shear is the factored shear the out-of-plane wall experiences, assuming the shear is constant along the height of each course of the wall (following CSA S304-14: 10.10.2). The shear resistance must exceed the design shear for the shear wall design to pass. This curve is drawn in blue in Figure 5‑82: Shear diagram ‑. The s hear resistance is the shear capacity of the shear wall, calculated based on CSA S304-14: 10.10.2. This curve is drawn in green, and extends from the top of the first course to the top of the wall.
The shear diagram corresponding to a specific load combination can be viewed by clicking on the Critical Load Envelope drop-down box. The drawing indicates at the top left corner the load combination that is used to determine that specific shear diagram.
A shear drawing with the design shear is available only for the critical load combination since this is the load combination the design shear is determined for. The actual shear and shear resistance can be view for all load combinations.
After achieving a successful axial, moment design, the program creates an axial resistance, Pr , vs. moment resistance, Mr , diagram. The P-M interaction diagram also displays the axial force, Pf , and the principal moment, Mf, every load combination, the program displays.
The calculation procedure and the curves displayed in the P-M interaction diagram depend on whether the wall is reinforced or not, and whether the masonry is hollow, partially grouted or fully grouted. The shape of the P-M diagram depends on the specific design. The general curve of the P-M diagram varies depending on if the shear wall is reinforced or not, depending on the grouting pattern (not grouted, partially grouted or fully grouted). The P-M diagram also depends on the loads applied. Is the wall designed a cracked wall? Can the tensile strength of the masonry be used? A concise discussion is provided in this section. Additional details are provided in the Appendix.
For unreinforced walls, moment resistance, Mr, is determined and plotted for incremented values of the axial resistance, Pr . The moment resistance calculations vary depending on whether the wall is designed as an uncracked or a cracked section. A full discussion on the possible P-M Diagram configurations for unreinforced shear walls is provided in the Appendix.
To view the P-M diagram:
A sample P-M Interaction diagram for a fixed-free supported reinforced, partially grouted wall is shown in Figure 5‑83: P-M Interaction Diagram for an Unreinforced, Fully Grouted Shear Wall .

Figure 5‑83: P-M Interaction Diagram for an Unreinforced, Fully Grouted Shear Wall
For drawings available in MASS , users are permitted to select the amount of detail displayed in each drawing. This feature becomes especially useful for P-M diagrams. With the Layers drop-down box, users can choose to include or exclude several P-M diagram features. For an unreinforced, fully grouted wall for instance, the following layers can be included or excluded:
The envelope curve (black line) indicates the moment resistance and axial resistance values used to achieve the design. To determine an exact data point on the envelope, place the mouse cursor on the black curve and left-click.
In addition to the resistance curves drawn in the P-M Interaction diagram, the program also displays the axial force and the factored moment (Pf,Mf).
The P-M interaction diagram for the shear wall design shown in Figure 5‑83: P-M Interaction Diagram for an Unreinforced, Fully Grouted Shear Wall is just one example. There are many other possible P-M diagram configurations. The shape of the P-M diagram depends on the specific design. For reinforced walls for example, the axial resistance, Pr , and the moment resistance, Mr, are determined and plotted for incremented values of the neutral axis depth,. The neutral axis depth begins with C mm and is incremented up by 1 mm with each iteration, terminating when the compression zone is equal to the thickness of the block (when β1c=t). MASS does not account for reinforcement in compression in the moment resistance calculations, since tying bars in walls is not easily accomplished.
The P-M Interaction diagram contains additional lines if the user chooses to apply loads in both directions (Section 5.2.3).
There are three tabulated result categories available in the shear wall module: simplified results, detailed results, and loads analysis results. The three result categories vary in the amount of detail provided, but all contain separate tables that approximately correspond to each design step, as shown in Figure 5‑84: Tabulated Results Categories for Shear Wall Module: Simplified, Detailed, Loads Analysis ‑.
Figure 5‑84: Tabulated Results Categories for Shear Wall Module: Simplified, Detailed, Loads Analysis
The simplified results show only those values that are required to give an overview of the results for a design criterion. The simplified results contain four tabs which provide design summaries for including:
The first three of tabs become available as soon as the moment design step is performed. The Shear tab is not available until the shear design step is performed. The Simplified Results tabs are updated at each design step to reflect any changes made to the wall design. The four Simplified Results tabs are not complete until all the design steps have been performed. For instructions on printing any the Simplified Results tab, the Detailed Results tab, or the Loads Analysis Results tab refer to Section Error! Reference source not found. .
The Shear Wall Properties tab is activated after the moment and deflection design are performed. To view the simplified results, wall properties:
The Shear Wall Properties tab contains a summary table (titled ‘Design Results Summary’) that quickly advises users of the design stages that have been satisfied. Design steps that have been satisfied, and provided a successful design, are indicated with a green check mark. The design steps that have been satisfied, but did not provide a successful design, are indicated with a red ‘X’. Design steps that are yet to be performed are indicated with a blue horizontal line. The shear wall designed in Section 5.2 with all design steps completed in shown in Figure 5‑85: Simplified Results (Shear Wall Properties, Design Step Status) .
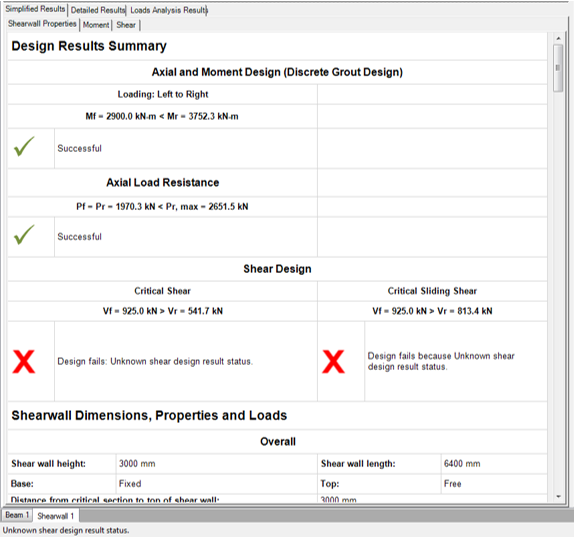
Figure 5‑85: Simplified Results (Shear Wall Properties, Design Step Status)
At the top of the design summary page, the axial and moment design steps are summarized. The program shows the maximum factored moment from the load analysis, and the moment resistance from the shear wall design, indicating if the design used the discrete grout or the smear grout approach. If the wall was loaded in one direction only, the program shows the factored moment and the moment resistance for a wall loaded form left to right. If the shear wall was loaded in both directions, the program shows the factored moment and the moment resistance for left-to-right, and for right-to-left loading. For the axial design, the program shows the maximum factored axial load, the axial load resistance (same as the factored axial load), and the maximum axial load resistance the shear wall is allowed to resist (CSA S304-14).
For shear design, MASS shows the maximum factored shear, critical shear resistance, and the critical sliding shear resistance.
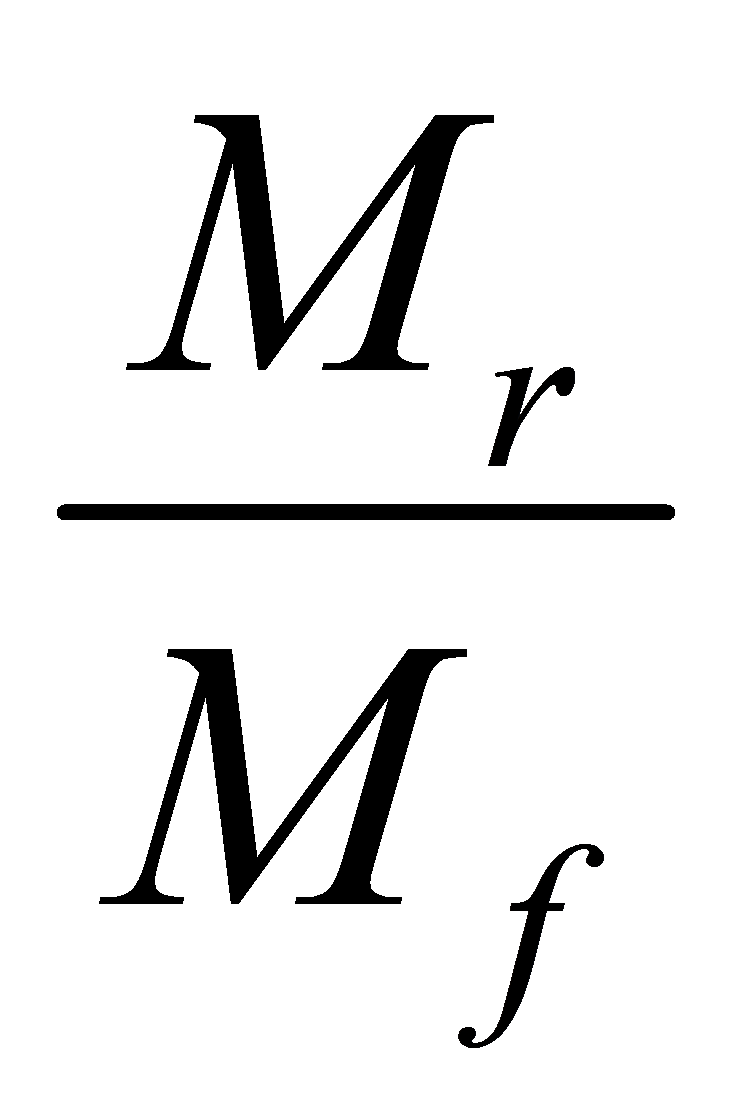
At the top of the design summary page, the moment design step is summarized. The program also shows the factored moment, Mf (for the critical load combination), and the moment resistance, Mr(for the critical load combination), indicating if the design used the discrete grout or the smear grout approach. While Mf is determined for every load combination, the critical load combination is the load combination that results in the smallest. This is the moment that the wall is designed for.
If the wall was loaded in one direction only, the program shows the factored moment and the moment resistance for a wall loaded form left to right. If the shear wall was loaded in both directions, the program shows the factored moment and the moment resistance for left-to-right, and for right-to-left loading.
The program also shows the factored axial load, Pf, the axial load resistance, Pr, and the maximum axial load resistance, Pr, max. The factored axial load is simply the factored applied axial load that corresponds to the critical load combination. For shear walls, the program sets the axial load resistance equal to the factored axial load, and solves for the neutral axis depth, C . Thus the axial load resistance is always be equal the factored axial load.
For information about the axial, and moment design strategies, refer to Section 5.5.1.
The maximum axial load resistance, Pr, max calculated in accordance to CSA S304-14: 7.4 (unreinforced walls) and CSA S304-14: 10.4 (reinforced walls).
For shear design, MASS shows the factored shear, Vf, the shear resistance, Vr and the at the critical section. The program also provides the factored sliding shear at the critical course, and the sliding shear resistance at the critical course. The critical section corresponds to the location along the height of the wall that results in the smallest Vf/ Vrratio. This may be different for shear and for sliding shear.
Scrolling down further along the ‘Design Summary Results’ page, the wall properties and the applied load information are provided. The wall properties provided include the wall dimensions, support information, masonry properties, as well as the unit properties used to attain the wall design ( Figure 5‑86: Simplified Results (Wall Properties) ‑).
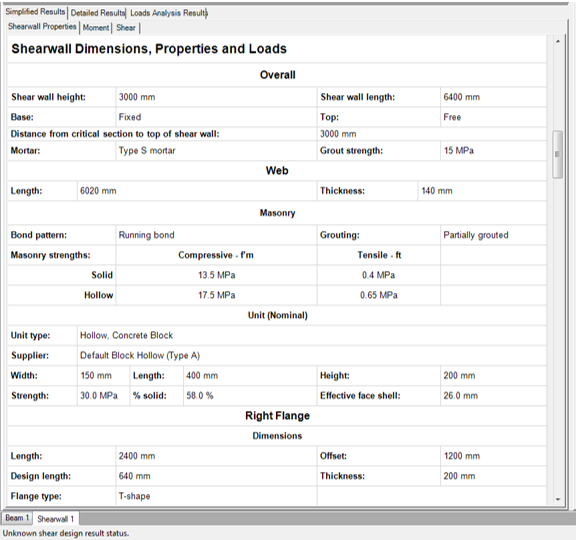
Figure 5‑86: Simplified Results (Wall Properties)
The applied loads information includes a list of all the loads applied to the wall (along with their location, unfactored magnitude, and percent sustained), a list of all the load combinations (used in the moment design step, and the shear design step), as well as a list of all the load types applied by users.
The Moment tab is activated after the moment design is performed. To view the simplified results, moment:
The M oment tab contains a summary table (titled ‘Moment Design Summary’) that quickly advises users of the success or failure of the moment design. A green check mark is used to indicate a successful moment design, as shown in Figure 5‑87: Simplified Results (Moment tab) . If the design is not successful, it is indicated with a red ‘X’.
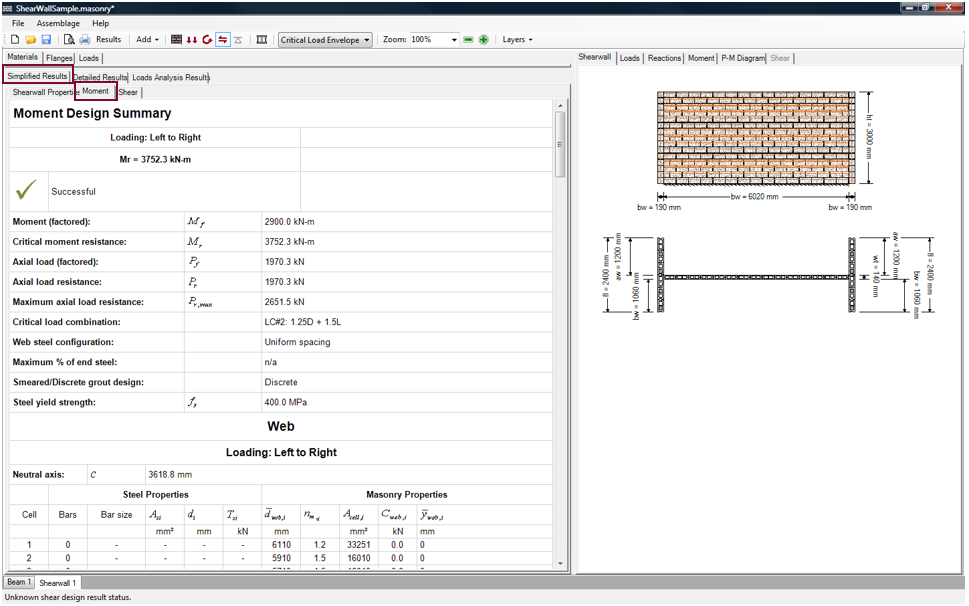
Figure 5‑87: Simplified Results (Moment tab)
At the top of the ‘Moment Design Summary’ page the factored moment, Mf, and the moment resistance, Mr , for the critical load combination are provided. The factored axial load (for the critical load combination),Pf , the maximum axial load resistance, Pr, the critical load combination, and the yield strength. The yield strength, fy, of the steel is simply the value entered by users (usually during the assemblage configuration design step). This value by default is 400 MPa.
The ‘Moment Design Summary’ page also provides the web steel configuration (uniform steel, concentrated end steel, cell-by-cell), as well as the maximum percentage of end steel permitted.
A further discussion on the web configurations can be found in Section 5.5.1.
The steel and masonry properties along the web are displayed on a cell-by-cell basis, including the bar size, bar area, Asi, depth to the bar (from the extreme compression fibre), di, tension force at each bar location, Tsi, distance from extreme compression face of wall to centroid of cell i in the web,  , modular ratio, nm,i, area of the cell, Acell,i, compression force at each cell, Cweb,i , and centroid of cell i in the web,
, modular ratio, nm,i, area of the cell, Acell,i, compression force at each cell, Cweb,i , and centroid of cell i in the web, .
.
Note: All tension bars that fall within the compression zone have zero tension. Vertical steel is not taken into account for compression calculations in the design process; as it is extremely difficult to tie the bars together in a cell of a concrete block masonry wall. As a result, when the steel goes into compression it is assumed to carry zero force because it is untied and can buckle. Therefore, the vertical steel is only be considered when in tension.
The steel properties of the reinforcement in each cell of each flange are also provided, as shown in Figure 5‑88: Simplified Results (Moment tab) ‑.
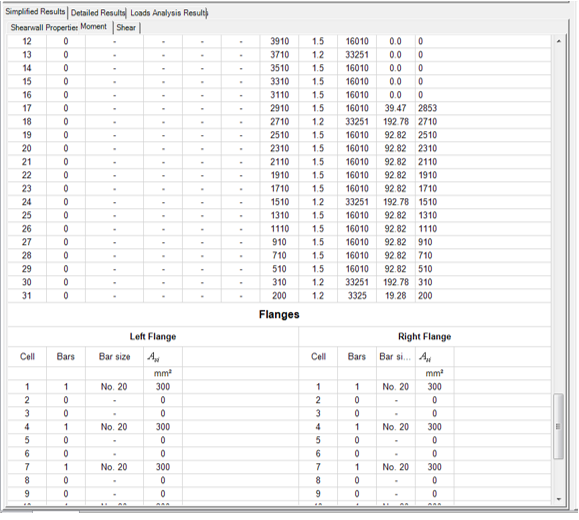
Figure 5‑88: Simplified Results (Moment tab)
The Shear tab is activated after the shear design is performed. To view the simplified results, shear:
The S hear tab contains a summary table (titled ‘Shear Design Summary’) that quickly advises users of the success or failure of the shear design (critical shear, and critical sliding shear). If the shear design step is satisfied, it is indicated with a green check mark; if not, it is indicated with a red ‘X’. See Figure 5‑89: Simplified Results (Shear tab) ‑.
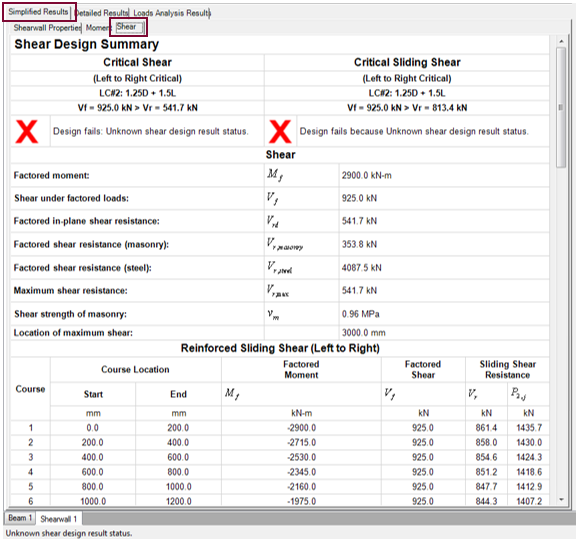
Figure 5‑89: Simplified Results (Shear tab)
At the top of the ‘Shear Design Summary’ page, the program provides the factored shear, Vf, and the critical in-plane shear resistance, Vrd , at the critical section, for the critical load combination. For in-plane shear, the critical load combination is the one with the smallest shear resistance to factored shear ratio along the wall height, Vrd/Vf. The critical section corresponds to the location along the height of the wall that results in the smallest Vrd/Vf ratio.

Note: The critical load combination may not be the same for moment design as it is for shear design.
The in-plane shear resistance itself,Vrd , is calculated by adding the factored shear resistance due to the masonry, Vr, masonry , and the factored shear resistance due to reinforcement,Vr, steel. The in-plane shear resistance is calculated in accordance to CSA S304-14: 10.10.2 for reinforced walls and CSA S304-14: 7.10.2 for unreinforced walls. It represents the resistance of the wall to diagonal cracking, as shown in Figure 5‑90: In-Plane Shear Resistance Resisted with Horizontal Reinforcement ‑. In order to increase the in-plane shear resistance of the wall the designer can provide additional shear (horizontal) reinforcement.
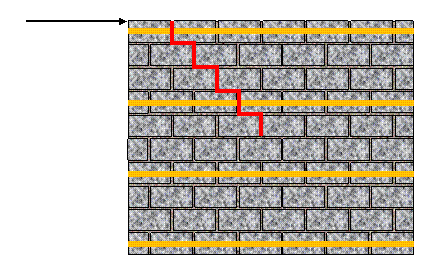
Figure 5‑90: In-Plane Shear Resistance Resisted with Horizontal Reinforcement
Scrolling further down the ‘Shear Design Summary’ page, the program also provides a table with the factored sliding shear, Vf , the critical sliding shear resistance, Vr,s , and the compression force, P1 (unreinforced shear walls), P2 (reinforced shear walls), at each course.
The program does not calculate the sliding shear at the base of the wall. It is the responsibility of users to verify the sliding shear resistance at the base of the wall, taking into account the friction coefficient of materials in contact (masonry-to-smooth concrete or bare steel), and dowels (if any). The sliding shear resistance between bed joints is calcul ated using CSA S304-04: 7.10.5 .1 (unreinforced wall) or CSA S304-14: 10.10.5 .1 (reinforced wall).
The critical load combination for each course is the one with the smallest shear resistance to factored shear ratio, at a specific location along the height of the wall, Vr,i/Vf,i.
The in-plane sliding shear resistance is calculated in accordance to CSA S304-14: 10.10.5.1 for reinforced walls and CSA S304-14: 7.10.5.1 for unreinforced walls. It represents the resistance of the wall to sliding, as shown in Figure 5‑91: In-Plane Sliding Shear Resisted with Vertical Reinforcement ‑. The sliding shear resistance is affected by the material in contact along the sliding plane (masonry to masonry, masonry to smooth concrete, or masonry to steel), the axial compression on the wall, and the clamping action of vertical reinforcing bars.
In order to increase the in-plane sliding shear resistance of the wall the designer can provide additional shear (horizontal) reinforcement.

Figure 5‑91: In-Plane Sliding Shear Resisted with Vertical Reinforcement
For shear resistance calculations, in accordance to Clause 7.10.1.3 and 10.10.1.3 of CSA S304-14, the program uses an upper limit on the factored shear resistance greater than the one given in Clause 7.10.2.1 and 10.10.2.1, respectively. For information about the shear design strategy, refer to Section 5.5.2.
In addition to the resistance to diagonal cracking, and sliding, the transverse shear resistance becomes relevant for shear walls that contain flanges or other boundary elements.
When a shear wall has flanges ( Figure 5‑92: Transverse Shear (NOT INCLUDED) ‑), these have to be connected to the web by: interlocking of the masonry units (50 % running bond), using horizontal reinforcement (joint reinforcement or bond beams) across the vertical intersection, or using rigid steel connectors fully embedded in mortar or grout (CSA S304-14: 7.11 and 10.11). Transverse shear calculations are not currently performed by MASS .

Figure 5‑92: Transverse Shear (NOT INCLUDED)
The intersection must be strong enough to withstand the shear forces acting vertically along the height of the wall and transverse shear resistance at the web-flanges connection.
The detailed results provide the intermediate calculations performed to obtain the final shear wall design. The detailed results are organized into tables that include:
The detailed results contain three tabs which provide design information for:
The first two tabs become available as soon as the moment design step is performed. The Shear tab is not available until the shear design step is performed. The Detailed Results tabs are updated at each design step to reflect any changes made to the wall design. The three Detailed Results tabs are not complete until all the design steps have been performed.
To view a full list of the shear wall properties:
The Shear Wall Properties tab contains a table that provides detailed information about the shear wall geometry, the reinforcement cover and spacing values, and any applicable constants and factors ( Figure 5‑93: Detailed Results (Shear Wall Properties) ‑). In general, the data presented in this Shear Wall Properties tab is common to more than one design step.
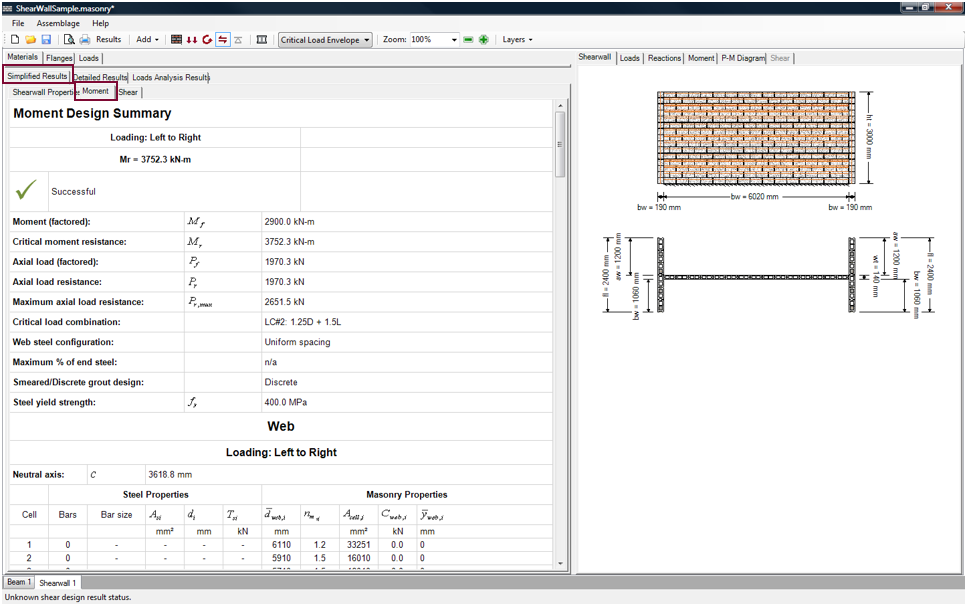
Figure 5‑93: Detailed Results (Shear Wall Properties)
Most variables displayed in the Detailed Results → Wall Properties tab are variables commonly used and follow the convention presented in CSA S304-14. In cases where the variable/symbol is not governed by a specific equation, a description of the variable is provided instead. The variables and equations that may require further explanation are discussed in the following subsections.
For partially grouted walls, users are permitted to apply smearing effects. Users are also permitted to concentrate the amount of steel placed in the web towards the ends. This typically results in several grouted cells towards the ends of the web. Smearing the grout in these cells with the cells in the centre of the web may result in a smaller calculated moment resistance. To take full advantage of the grout at the ends, the web is divided into three segments: the smeared segment and the two ends. The program refers to these two ends as end zones. Within the engineering calculations, an end zone is defined by the number of consecutively cells at either end of the web, and is terminated at an empty cell, as shown in Figure 5‑94: Smeared Segments vs. End Zones ‑.
If a user manually removes the grouting of the first cell in an end zone, there will be no end zone on that side of the web. That portion of the web is then included in the smeared section of the wall.
A partial cell can be included in the length of the end zone if it is grouted.

Figure 5‑94: Smeared Segments vs. End Zones

Note: Smearing effects can be applied even if there are no end zones. If there are no end zones, the entire length of the web is smeared. Refer to Section 5.2.1.
As discussed in Section 5.2.1, MASS allows two methods to determine the axial and moment resistance of the shear wall; the discrete method, or the smeared-grout method. When the discrete method is applied, the program determines the compression resistance for each cell and adds them together to determine the axial resistance of the shear wall. The moment resistance is also evaluated cell-by-cell; the program uses the compression resistance for each cell, and determines the centroid of each cell to calculate the moment arm.
When the smeared grout method is applied, the program separates the web of the shear wall into segments: end zone 1, end zone 2, and the smeared section. The length of the smeared segment is determined as follows
The program uses these segments and the compression resistance of each separately, and adds them together to determine the axial resistance of the shear wall. The smeared section uses an effective compressive strength,Fm,eff, web, and its area is defined by an effective thickness, teff. The effective thickness, teff, represents the equivalent grout thickness if the grout in a partially grouted wall is smeared along its length. The moment resistance is also evaluated using the three sections (end zone 1, end zone 2, and the smeared section); the program uses the compression resistance for each section, and determines the centroid of each section to calculate the moment arm.

Note: The program does not allow using the smearing effects with unreinforced, ungrouted shear walls. For fully grouted shear walls, applying smearing effects does not affect the design. The effective thickness is the same as the width of the shear wall, and the grouted compressive strength is used, yielding the same design as users obtains using the discrete method.
The actual length of a flange is equal to the flange overhang(s) plus the width of the shear wall web. This is the value the designer enters in the ‘Length’ textbox demonstrated in Figure 5-23). However, in the program, the effective flange length, as indicated by CSA S304-14: 10.6.2) is limited. The program uses the lesser of:
Limiting the effective length of the flanges can be conservative for combined flexure and axial resistance calculations, but it ensures that the shear wall has ample reserve shear capacity to accommodate an increase of lateral loads, especially for unreinforced walls.
In masonry design, the stress orientation factor is used when the equivalent rectangular stress block is used (cracked section design of beams, walls, and shear walls). It accounts for the direction of compressive stress and the continuity of grout in masonry elements.
The compressive strength of masonry, Fm, is determined for compression normal to the bed joint in a member. When the compression stress is applied parallel to the bed joint the values for compression strength are lower. The compressive strength, Fm can be multiplied by the stress orientation factor to account for this. For compression normal to the bed joint, X =1.0 ; for compression parallel to the bed joint, X =0.5 , unless grout is continuous in the direction of the compressive force (cavity between wythes, or when lintel or knockout web blocks are used), in which case, X =0.7 .
As in concrete design, the rectangular stress block can be used in masonry design to simplify calculations of the resultant compression force at ultimate strength. The ratio of depth of rectangular compression stress block to depth to neutral axis,B1, helps define the rectangular compression block.
B1 is 0.8 for masonry compressive strength values equal and less than 20 MPa. For compressive strength values greater than 20 MPa, B1 decreases at a rate of 0.1 for each increase of 10 MPa above 20 MPa compressive strength, following CSA S304-14: 10.2.6. For unreinforced walls, this factor is calculated using f’m,hollow, for an ungrouted wall and f’m,grouted for a grouted wall. For reinforced walls, this factor is calculated using the minimum off’m,grouted, f’m,grouted , and f’m,eff to maintain a conservative design.
Since MASS allows shear walls to have flanges of different physical properties than the web, there is a specific B1 for each flange and the web (B1, flange1,B1, flange2, and B1, web). In the shear wall module, the program uses a different B1 value depending on if the compression zone falls within flange 1, flange 2, or the web.
For a shear wall composed of hollow ungrouted blocks, or semi-solid ungrouted blocks, or solid blocks, the compressive strength values are readily obtained from CSA S304-14: Table 4. In MASS when ignoring the effects of grout, the compressive strength value used is f’m,hollow . In MASS , when including the effects of grout for grouted walls, the compression strength of the masonry depends on the depth of the compression zone. If the depth of the compression zone falls in the face shell, the values for the hollow compressive strength, f’m,hollow , can be used (CSA S304-14: Table 4). If the depth of the compression zone is greater than the width of the face shell, and the wall is fully grouted, the values for grouted compressive strength, f’m,grouted , can be used (CSA S304-14: Table 4). If the depth of the compression zone is greater than the width of the face shell, and the wall is partially grouted, an effective compressive strength, Fm,eff, is calculated. The weighted average compressive strength (effective compressive strength, Fm,eff ) is determined by averaging the compressive strengths of the grouted cells (f’m,grouted ) and the ungrouted cells (f’m,hollow ) with respect to the relative areas:
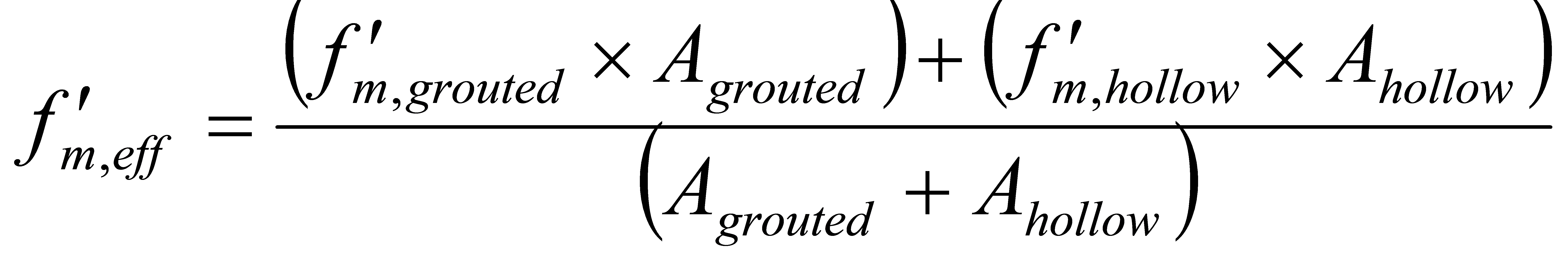
Where Agrouted is the grouted cross-sectional area of the wall, and Ahollow is the hollow cross-sectional area of the wall. The effective tensile strength can be calculated using the same principles.

Note: This feature only affects the engineering calculations for partially grouted webs. For webs that are not grouted, Agrouted =0 therefore f’m,eff = f’m,hollow . For webs that are fully grouted, Ahollow =0 , therefore f’m,eff = f’m,grouted.
For axial and moment design of shear walls the use of a specific compressive strength depends on the calculation method employed. If applying the discrete method, the program uses the hollow compressive strength (f’m,hollow , web) if the cell is not grouted, and the grouted compressive strength (f’m,grouted ,web) is the cell is fully grouted. If applying smearing effects, the program uses an effective compressive strength (f’m,eff,web). For the flanges, the program uses f’m,hollow,flange1 and f’m,hollow,flange2 if they are hollow; f’m,grouted,flange1 and f’m,grouted,flange2 if they are fully grouted; and, f’m,eff,flange1 and f’m,eff,flange2 if they are partially grouted.
The face shell thickness refers to the width of the face shell, or portion of a block between cell and outside surface of block side. Face shells are often tapered or flared as shown in Figure 4-59, so have varying thickness over the height of the block. The flare is introduced to facilitate picking up the block. In general, face shell thickness depends on block size, with wider blocks having proportionately larger face shells.
The effective face shell thickness, tf, of the block is the thickness to be used for design. It is the face shell thickness that develops from the placement of face shell mortar between the masonry units, and should not be confused with the actual minimum, average, or maximum thickness of the block shell.
The maximum face shell thickness is not displayed by the program, and cannot be altered by users. However, it is required by the program to determine the available space into which reinforcing steel bar can be placed. That is, the maximum face shell thickness is considered only indirectly; it is incorporated in the limits and tolerances on user input of steel bars in the cell cavities.

The effective area of masonry (Ae,transformed ) and the centre of mass () of the uncracked section are variables affected by the presence of weaker materials in the shear wall assemblage. In shear wall design, the program allows the use of flanges in the axial load and moment resistance calculations. Since, the program also allows having flanges with different masonry properties than the web of the shear wall, the calculation of some variables includes a modular ratio (nm) to account for weaker materials.
The modular ratio represents the ratio of elastic modulus of masonry (Em,web, Em,flange1, Em,flange2, Em,web,endzone, Em,smear,web) to elastic modulus of the weakest masonry in the assemblage, that is:
The program determines a modular ratio for each section of the shear wall (
nm,web, nm,flange, nm,flange2, nm,endzone,web, nm,smear,web ). Given that the modulus of elasticity is directly related to the compressive strength of masonry, it depends on the unit strength used in a particular section, and the level of grouting (hollow, or fully grouted).
To view a full list of the moment design results:
The Moment tab contains a table that provides the equations and data related to the axial and moment resistance calculations for the designed shear wall. If users chooses to apply the loads in both directions, this tab shows both sets of data.
In general, the data presented in this Moment tab approximately corresponds to the calculations performed in the moment design step. The detailed moment results are available upon the completion of the moment design step. Once again, it is possible for the moment design results to change after the completion of the shear design step. This is why it is recommended the designer completes all the design steps before moving on to viewing the results in too much detail.
The first set of variables displayed are the final, summarized axial resistance calculations for the wall design. Further down, the moment resistance calculations are presented, as shown in Figure 5‑95: Detailed Results (Moment) . As mentioned in Section 1.1.1 Drawings , MASS employs a unique design approach; the program allows users to apply loads in both directions.
Note: The two sets of axial resistance calculations (for both loading directions) are only provided if users specifically selected to ‘Apply loads in both directions’ (Section 5.2.3)
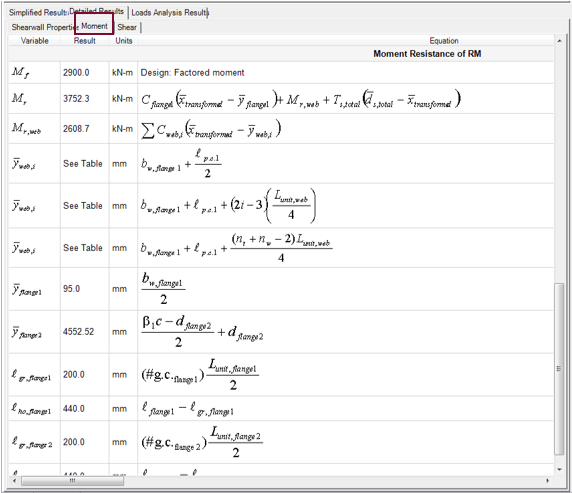
Figure 5‑95: Detailed Results (Moment)
Notice, also, that for some variables, under the ‘Result’ column, no numerical value is provided. Instead the entry states ‘See Table’. This refers to the cell-by-cell properties table shown in the Simplified Properties → Moment tab ( Figure 5‑87: Simplified Results (Moment tab) ‑).
Most variables displayed in the Detailed Results → Moment tab are variables commonly used and follow the convention presented in CSA S304-14. In cases where the variable/symbol is not governed by a specific equation, a description of the variable is provided instead. Variables and equations that require further explanation are discussed in the following subsections.
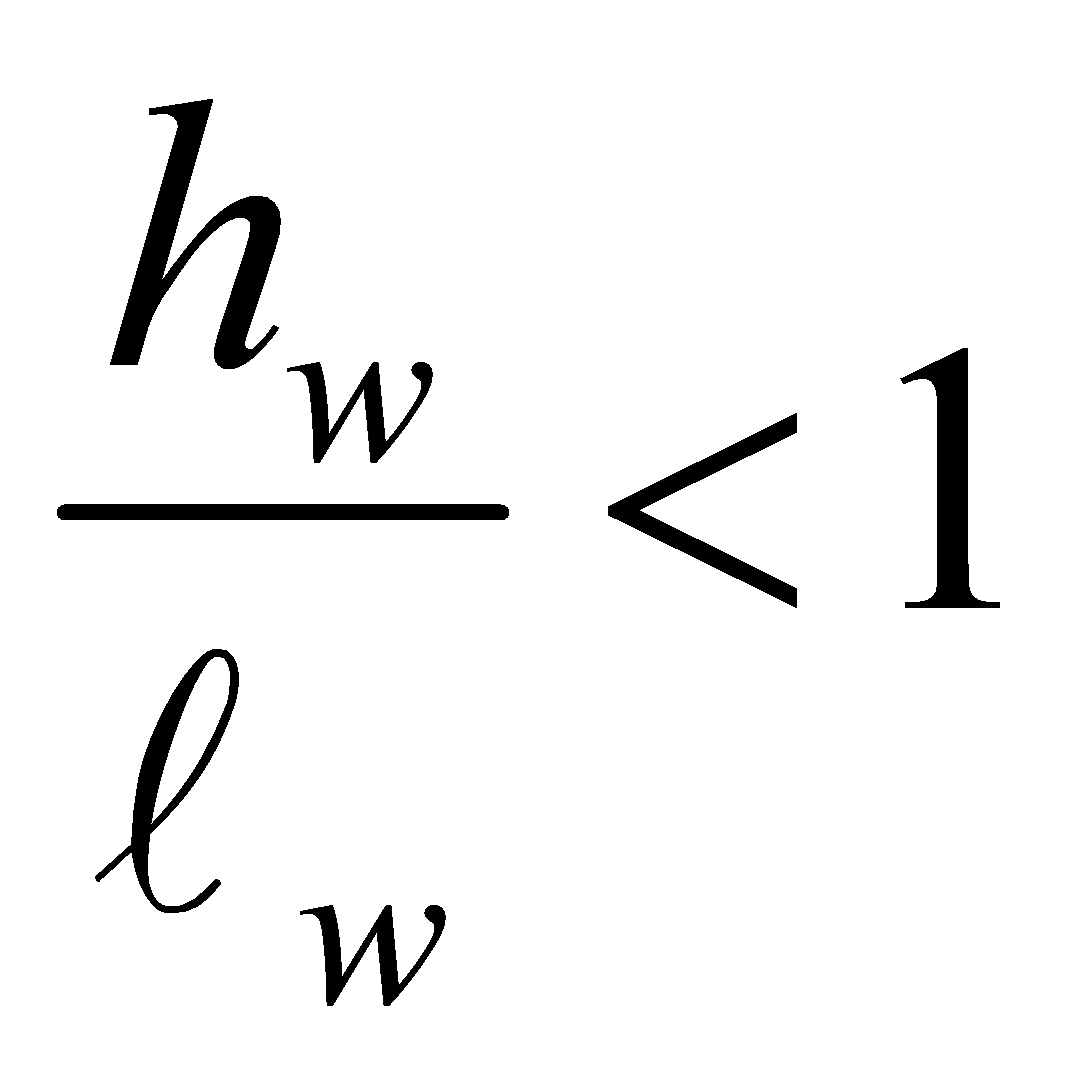
In the program, low aspect ratio ( squat ) shear walls (where), follow a similar design strategy as normal shear walls; however, some special requirements are taken into account in the moment, and shear resistance calculations.
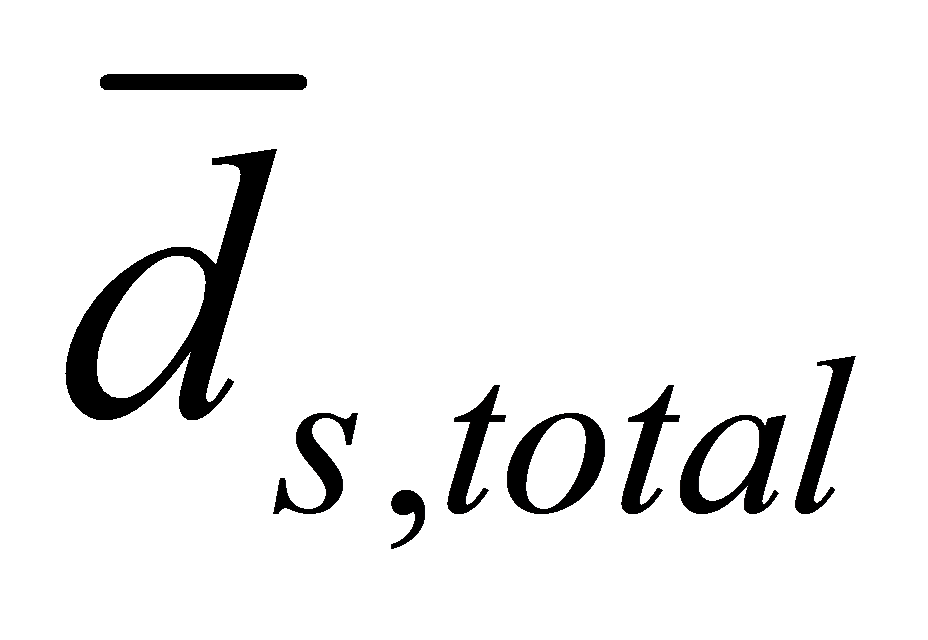
In accordance to CSA S304-14: 10.2.8, low aspect ratio (squat) shear walls are designed as deep sections. For moment resistance calculations, the program uses a reduced moment arm between the compression zone and the tensile reinforcement in the wall. The program determines the effective depth of the tension reinforcement, , including flanges, and ensures that the obtained value is less than, or equal to, the minimum of 0.67ℓw and 0.7hw.
For unreinforced walls, the Detailed Results → Moment tab shows information about the uncracked and (or cracked) properties of the shear wall, as can be seen in Figure 5‑96: Eccentricity Limit ‑.

Figure 5‑96: Eccentricity Limit
For unreinforced walls, the program verifies if the wall can be designed as a cracked section by determining the virtual eccentricity limit elimit=t/3 (CSA S304-14: 7.2.3) and comparing it to the actual virtual eccentricity e=Mf/Pf. That is, if elimit the wall can be designed as a cracked section, if e ≥elimit the wall must be designed as an uncracked section.
Notice, that depending on if the wall is cracked, reinforced, and the eccentricity, a different moment equation may be used, as presented in Table 5‑3: Moment Resistance of Unreinforced Shear Walls ‑. The equations presented in Table 5‑3: Moment Resistance of Unreinforced Shear Walls ‑ are generalized. The variables will vary slightly depending on if the shear wall contains flanges or not.
Table 5‑3: Moment Resistance of Unreinforced Shear Walls
| Symbol | Equation | Description |
 |  | A wall designed to remain uncracked carries a compressive masonry strength, as well as a tensile masonry strength (unlike cracked walls, where the tensile strength of masonry is neglected). The moment resistance of an uncracked section is determined by comparing the tensile and compressive strength of masonry. The smaller of these two values is taken as the moment resistance of the wall. |
 | 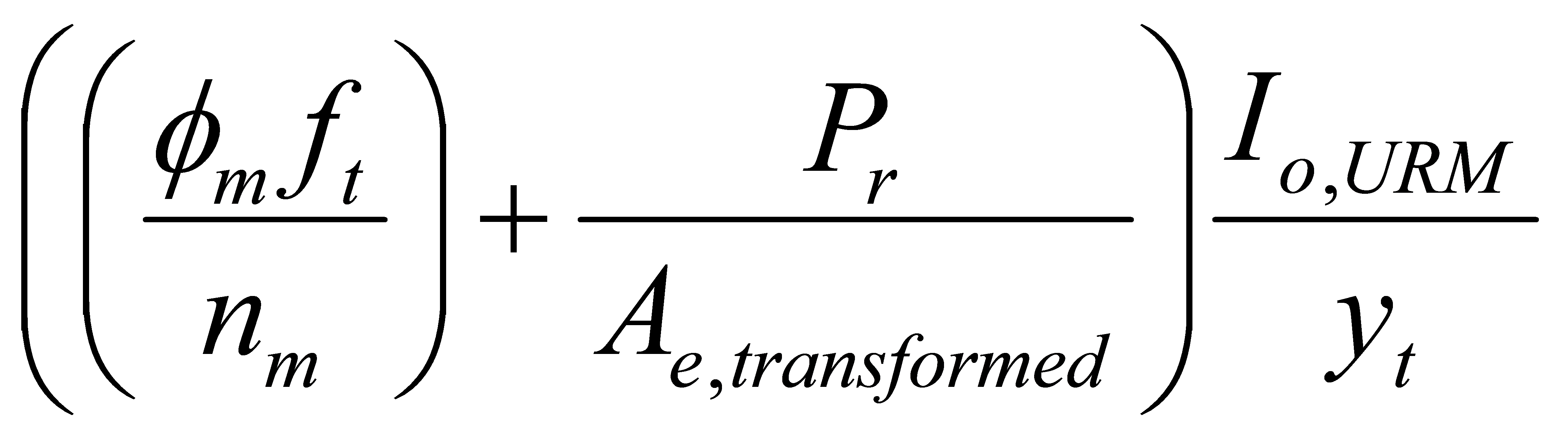 | Factored moment resistance based on the tensile stress. This equation can only be used if wall is designed to remain uncracked. |
 | 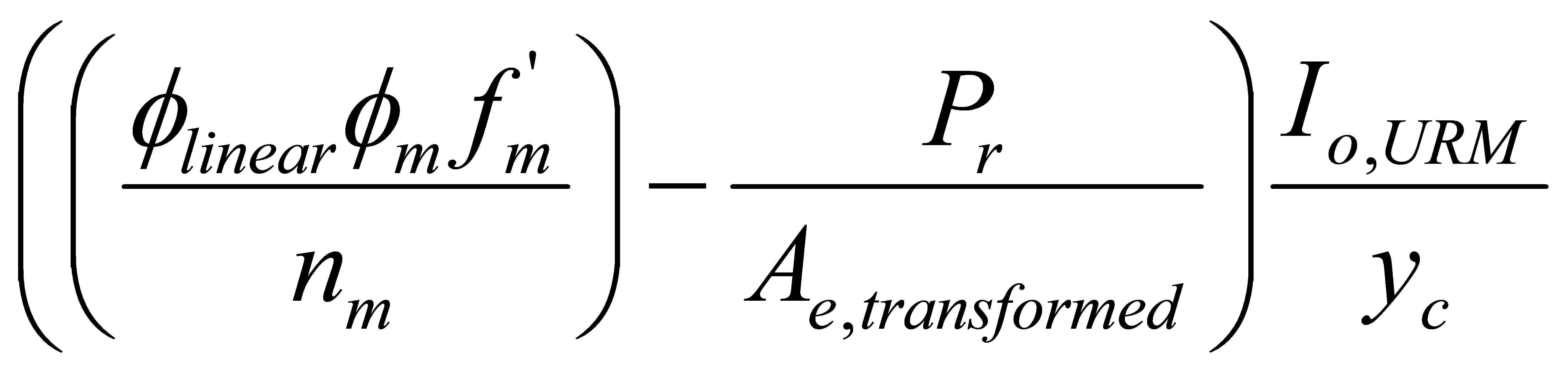 | Factored moment resistance based on the compressive stress. |
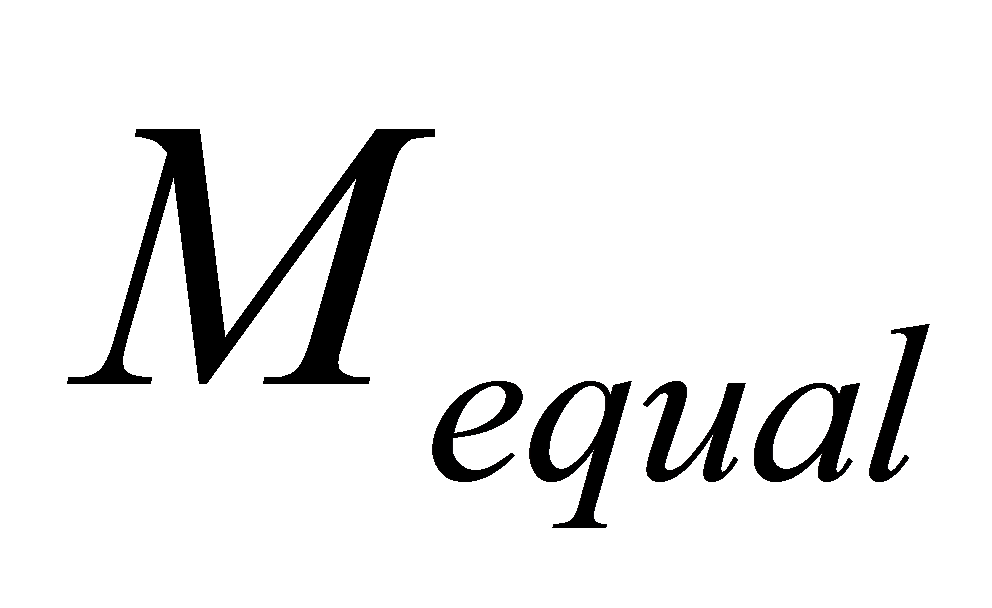 |  | This equation creates the cut-off point where the tensile strength of the wall can no longer be used. This occurs at the value , when the compressive strength of the masonry and the tensile strength of the masonry are equal. |
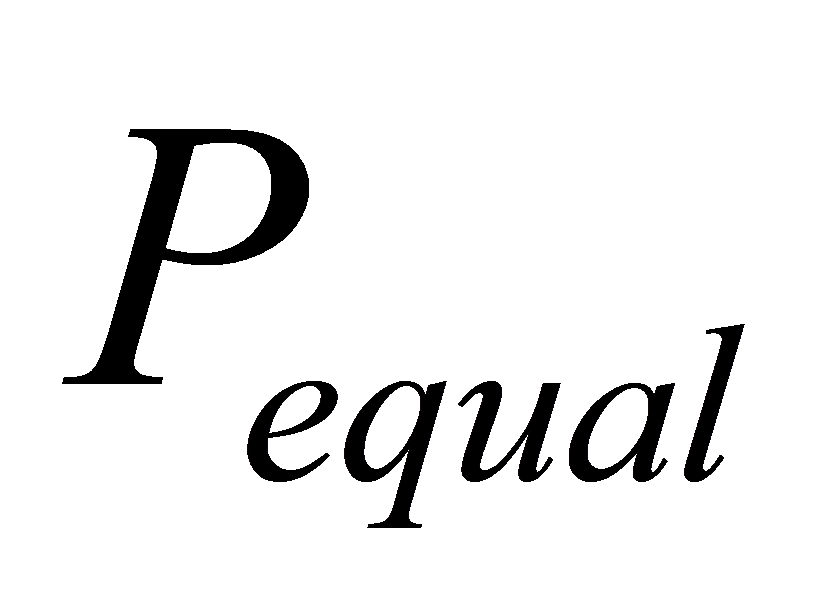 |  | This equation creates the cut-off point where the tensile strength of the wall can no longer be used. This occurs at the value , when the compressive strength of the masonry and the tensile strength of the masonry are equal. |
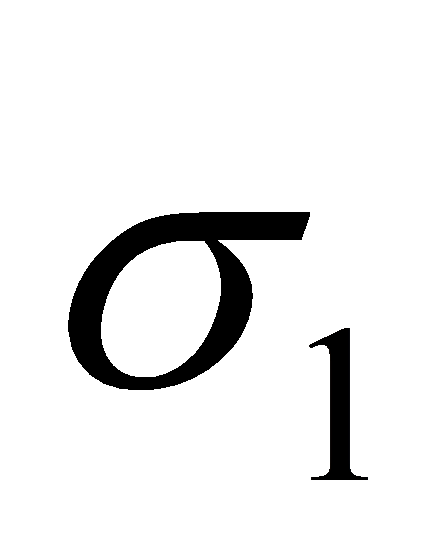 |  | Stress in the masonry on the compression side. |
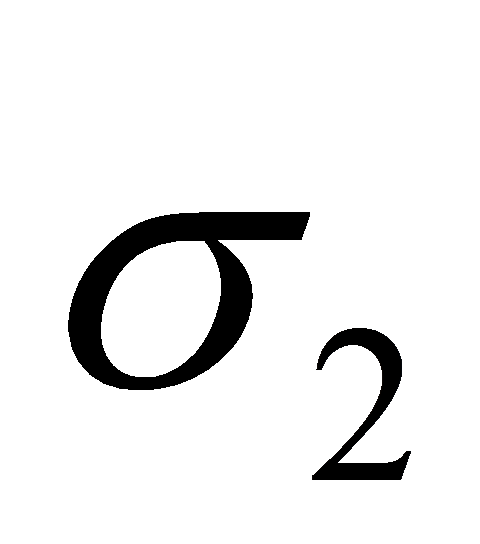 |  | Stress in the masonry on the tension side. |
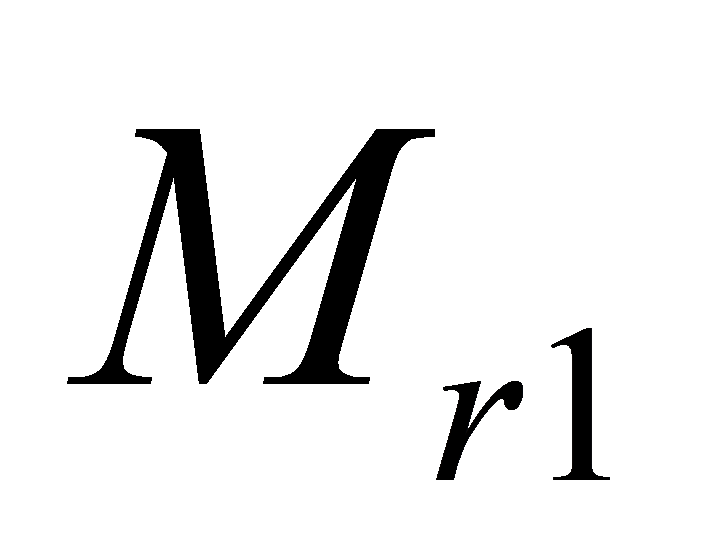 |  | Factored moment resistance for a wall that can be designed as a cracked wall. A wall that can be designed as a cracked unreinforced wall carries a compressive masonry strength only. The corresponding masonry strength is compared to the moment along the line (governed by CSA S304-14: 7.2.3), and the smaller of the two values is used. |
For more information, refer to the Appendix.
To view a full list of the shear design results:
The Shear tab contains a table that provides detailed information about the shear design calculations, as shown in Figure 5‑97: Detailed Results (Shear) . The program shows factors, variables, and equations for the shear and the sliding shear at the location of the critical section.
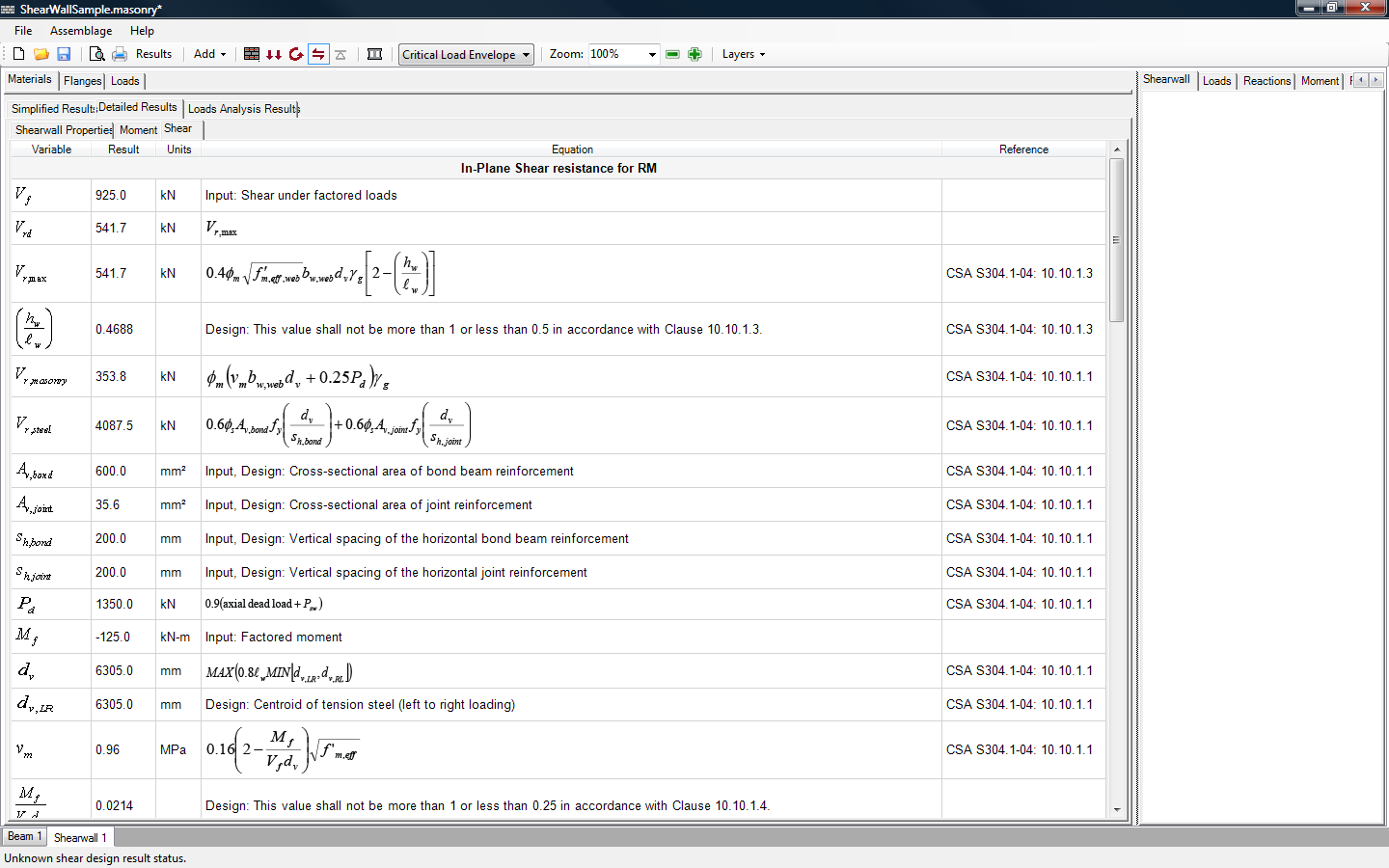
Figure 5‑97: Detailed Results (Shear)
In general, the data presented in this Shear tab approximately corresponds to the calculations performed in the shear design step. The variables displayed in the Detailed Results → Shear tab are variables commonly used and follow the convention presented in CSA S304-14. Two exceptions may be the effective compression area, Auc, and the effective depth, dv.
The sliding shear resistance of unreinforced shear walls depends on the bond strength at the joints, and the friction force between the materials. The bond strength is affected by the compressive strength of masonry and the uncracked portion of the effective area under compression, Auc. Since it is very difficult to determine the extend of cracking within the wall, the program compares the factored moment (Mf,j) to the cracking moment (Mcr,j), at each bed joint location; if the factored moment exceeds the cracking moment, the program assumes the entire cross-sectional area has cracked, and uses Auc=0 for the sliding shear resistance calculation of that particular joint.
The effective depth can be determined by calculating the resultant steel tension force:
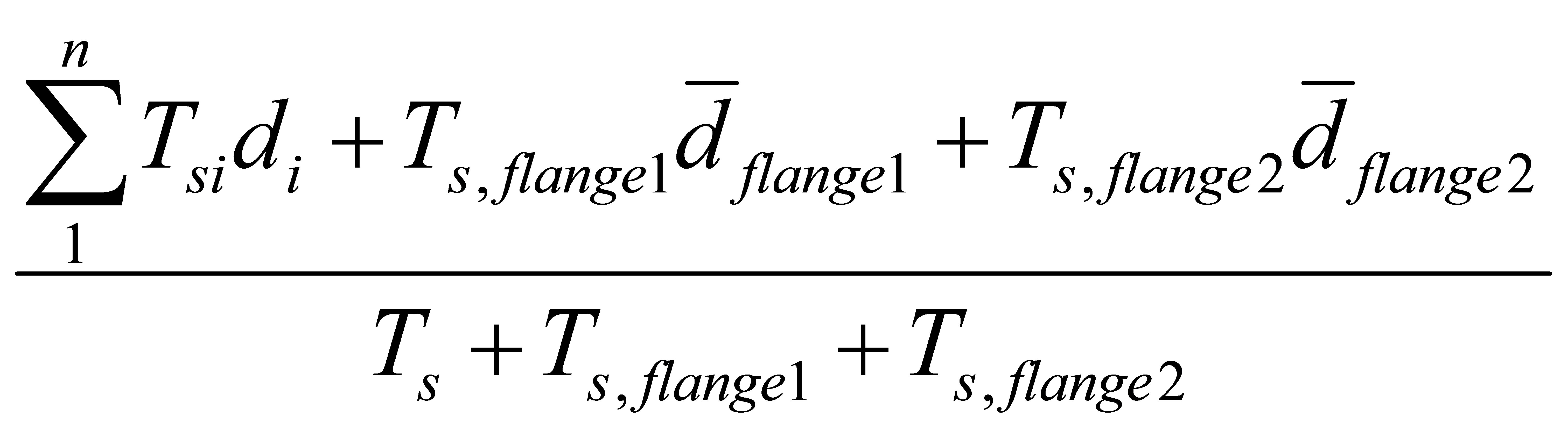
If the user has selected to ‘Apply loads in both directions’ (Section 5.2.3), the program calculates the resultant steel tension force with respect to both directions.
If users have selected to design the shear wall in one direction only, the effective depth for right-to-left loading is set to zero.
To remain conservative, the minimum of these values is selected. The effective depth calculated is compared to 0.8ℓw (CSA S304-14: 10.10.2.1). The greater of the two is used as the effective depth,dv.